Cushioning materials
Formerly: Cork
Cork used to be as favoured as an anti-vibration material due to the springiness caused by the compression and expansion of the trapped air. The air is gradually displaced from the cork, however, diminishing its isolating effect. Cork is hygroscopic and only allows low levels of spring excursion therefore this material is not in such widespread use today as it was in the past, at least not in heavy-duty applications. The same can be said for felt which, generally speaking, has similar properties.
Today: steel and rubber
The cushioning materials which are the preferred choice today are steel and rubber. Steel springs usually come in the form of flat coil springs and leaf springs. The advantage of steel strings is their relatively high load tolerance, but the disadvantage is that they are very limited in terms of their damping effect. This is also why major problems arise in the resonant range, often requiring special precautions to be taken to limit the spring excursion. In contrast to steel, rubber has a high level of internal damping. Rubber absorbs sound and boasts good elasticity and chemical resistance. These properties make rubber a particularly functional cushioning material.
The stress-strain graphs below clearly illustrate the different elongation properties of different materials. Fig. 1 relates to a tensile test with steel, while Fig. 2 is the result of the same test with rubber.
Steel
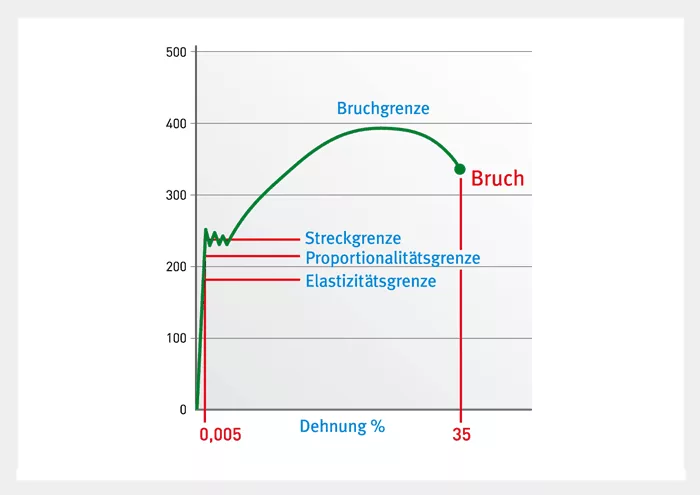
With steel, the load rises in a straight line up to the proportionality limit. Hooke’s law of elasticityapplies up until this point in that the stress is proportional to the strain, and the proportionality constant is equal to the modulus of elasticity. Up until this point the steel is elastic and will return to its original form when relieved of the load. The material begins to stretch at the elastic limit or yield point limit, a little above the proportionality limit, without any increase in the tensile force. The maximum tensile force is reached at the breaking point. The fracture occurs after further stretching, but at a lower tensile force because the cross section has become smaller.
Rubber
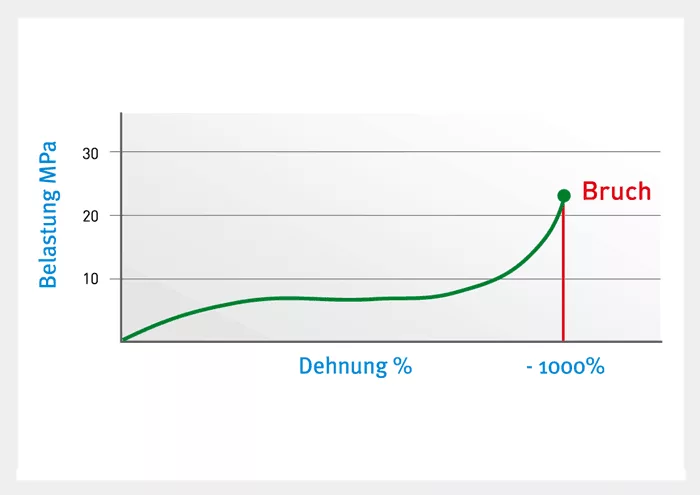
The sequence is completely different with rubber. The elongation of the rubber is already high at a very low level of tensile stress. Nor does the stress rise in a straight line, i.e. rubber does not stretch in proportion to the load. This means that the modulus of elasticity is not constant and therefore Hooke’s law does not apply either. There is no yield point; the stress rises until the break suddenly occurs.
Further information
Rubber as a building material
Rubber has special properties compared to other building materials. The elongation can be more than 1,000% in certain cases and for the most part in the elastic range. Metals, on the other hand, have very small strain values below the elastic limit.
Design aspects
With hard rubber you can increase the strain a little. The connection of rubber with metal is not a weak point and stronger than the rubber itself.
Principle Constellations
In principle, elastic intermediate layers, i.e. vibration dampers, are installed in practice for two different reasons: Practical considerations and protective considerations.

