Rubber as a construction material
Rubber has special properties to offer in comparison with other construction materials. The elongation in some cases can be more than 1,000% and for the most part in the elastic range. Metals, by contrast, have very low strain values below the limit of elasticity.
The tensile strength of rubber is fairly low, however, in comparison with metals. The maximum which can be reached with rubber is 25-30 MPa. Due to its high stretching properties, however, rubber has a very high working capacity in contrast to the best grades of steel. If a body is subject to load below the limit of elasticity, the strain will be proportional to the load according to Hooke’s law of elasticity. This applies to rubber under tension and pressure and means that rubber does not have a constant modulus of elasticity in extension or compression.
Metals usually become more pliable towards the end of a tensile test. The reaction in rubber is usually the opposite. Rubber has no yield point, and the modulus increases until the break suddenly occurs.
A
The high level of elasticity is therefore the most eminent property of rubber. The ease with which rubber can be deformed is indicated by the fact that the modulus of elasticity in compression for rubber within the normal hardness range of 30-80°IRH is between 2 and 12 MPa while the comparable modulus of elasticity for steel is 210,000. This means that soft rubber is about 100,000 times more pliable than steel.
B
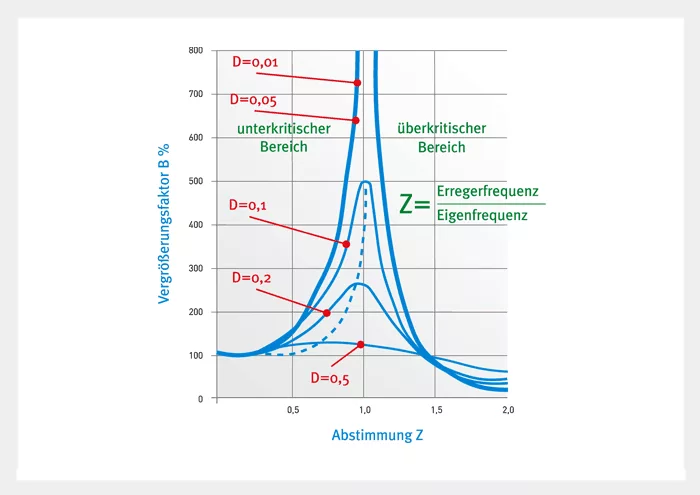
The buffering capacity of rubber is another important property of the material. It is of particular significance if the resonant range is traversed by a machine mounted on springs.
The resonant travel of a rubber spring is 1/5-1/50 compared with the travel of a steel spring of the same rigidity.
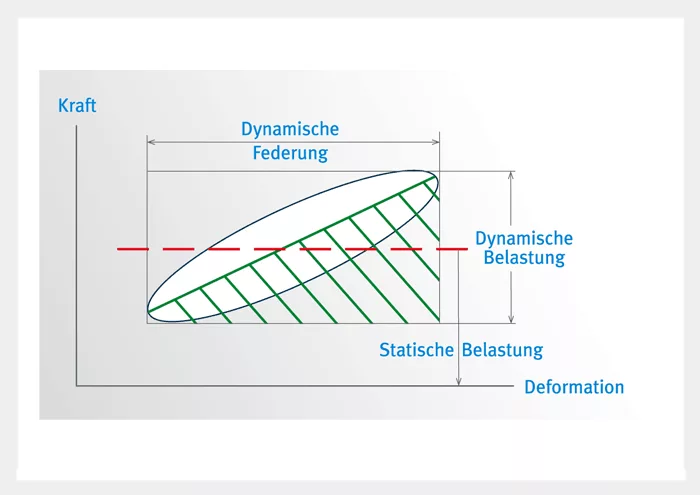
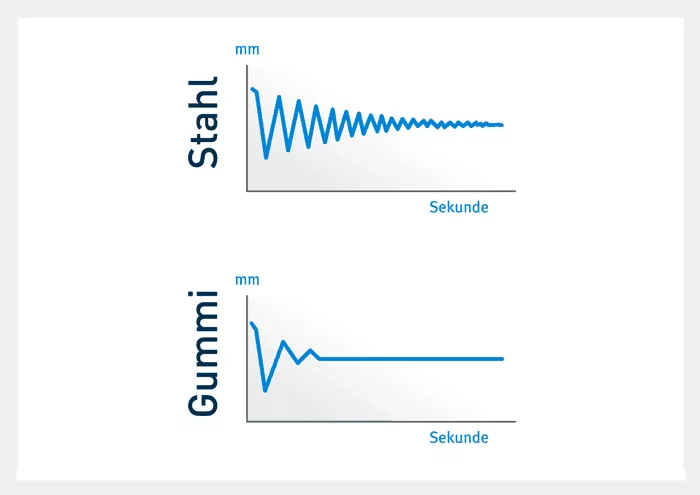
If a rubber spring is subjected to pressure or thrust, the direct energy loss is between 6 and 30%, depending on the hardness of the rubber. This is sufficient for the rubber springs to be used as vibration dampers in many cases. It is important, however, to be careful with the damping action in a rubber shock mount. If load levels are high, a large amount of energy will be converted to heat, which can lead to the destruction of the rubber mount (Fig. 4). Fig. 5 shows the vibration response to single jolts and jerks. The first graph shows the response of a steel spring and the second graph the response of a rubber spring. The graphs show clearly how quickly the vibrations subside in the rubber and how slowly they die out in the steel springs in comparison.
C
Rubber is one of the best sound insulation materials. The sound insulation increases with the thickness of the rubber. Rubber is excellent at cushioning structure-borne noise which is generated in base plates, floors and buildings, etc.
D
The high chemical resistance of the rubber is another valuable quality in favour of its use as a cushioning material. Steel springs, by contrast, are easily corroded by humid air and acids.
Rubber is entirely resistant to humid air and commonly occurring acids. The highest temperature to which natural rubber can be continually exposed is about +75°C. Rubber becomes rigid in very low temperatures of between 30 and -40°C, and at even lower temperatures the material becomes very hard, brittle and inelastic. Vibration dampers which may come into contact with oil therefore need to be made of synthetic oil-resistant rubber, but the cushioning properties of this are worse than those of natural rubber. The detrimental effects of oil can be avoided, however, by fitting a mechanical protection or by applying an oil-resistant coating to the rubber.
Further information
Spring material
In the past, cork was usually used as a springy material, the springiness of which was due to compression and relaxation of the trapped air. The spring materials that are coming to the fore today are steel and rubber.
Design aspects
With hard rubber you can increase the strain a little. The connection of rubber with metal is not a weak point and stronger than the rubber itself.
Principle Constellations
In principle, elastic intermediate layers, i.e. vibration dampers, are installed in practice for two different reasons: Practical considerations and protective considerations.

