Design aspects
With reference to calculating the deformation of rubber under pressure, it has already been mentioned that the resilience is not directly proportional to the load but that the modulus of elasticity in compression increases with the stress. The modulus of elasticity in torsion, by contrast, is constant under normal load.
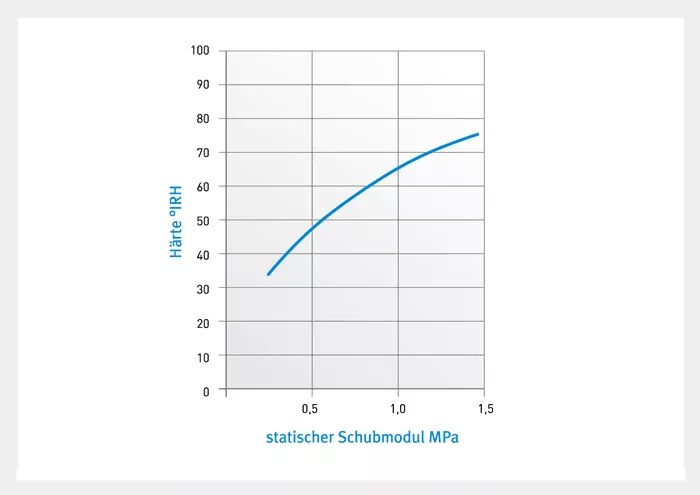
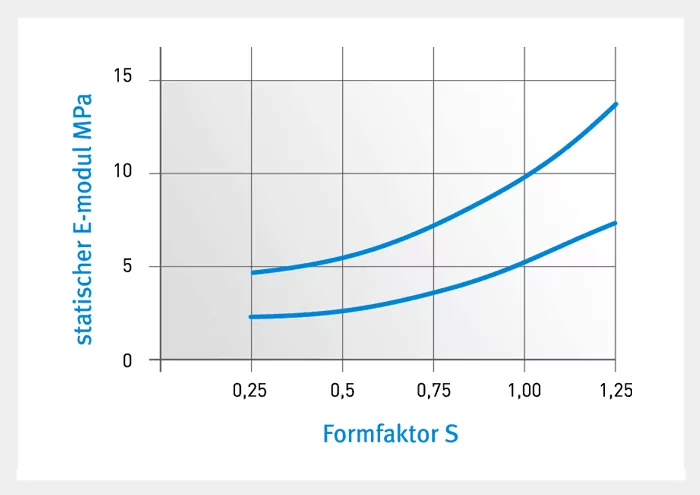
The most important factor for the modulus of elasticity is the ratio of surface under load to surface not under load. This stress concentration factor (denoted by S below) has a major influence on the modulus of elasticity in a rubber spring. Very thin rubber can have an extremely high modulus of elasticity ES=EO (1+2 – konst * S2). The rigidity of a rubber spring is also affected by its dimensions and by the hardness of the rubber.
Fig. 1 shows the relation between the hardness of the rubber and the modulus of elasticity in torsion, while; Fig. 2 plots the modulus of elasticity in compression against the stress concentration factor.
The above graphs apply in case of 10% deformation. The graphs show that rubber is about 6-8 times as soft against shear force with a stress concentration factor of 0.25 and with the same rubber hardness. Rubber is best used as a spring if shear force is envisaged because pressure is only likely to be 3-4 times the stress of shear force. Furthermore, the modulus of elasticity in torsion does not change to any significant degree subject to load and shape therefore this is generally the preferred choice of load today for rubber springs if high resilience is required. A high level of spring excursion means good isolation especially at low vibration generator frequencies. The stated modulus values apply in a static compression test in which the abutting faces cannot slide. If rubber is subjected to rapid vibrations, it will behave as if it were more rigid than it is. A rubber spring therefore generates a static and a dynamic spring constant. The dynamic spring constant depends on the frequency and amplitude. The effect of the amplitude is such that the rubber buffer will stiffen as the amplitude decreases. The majority of the items mentioned undergo dynamic testing and have an amplitude of 0.05 mm. The ratio of dynamic to static stiffness depends on the material and the geometric shape of the buffer.
The ratio is between 1.2 and 1.9 for the vibration absorbers listed in this catalogue. The detailed data sheets for each individual line of vibration absorbers contain design calculations based on the dynamic spring constants tested in the laboratory.
One very important question is how long the rubber may be subjected to continuous stress. An amount of 0.25 MPa is usually regarded as a normal level of shear force, but this can readily rise to 0.5 MPa in certain cases.
Higher shearing loads are pointless as the shear stress will easily cross over into tensile stress.
In our experience, tensile stress is very bad for rubber-metal connections. If these connections are subjected to high shearing loads, the rubber will need to be pre-tensioned slightly. Compressive stress is usually calculated at 1 MPa for rubber fittings attached to metal although there is a limit in that the deformation must not be greater than 20-25%.
The load can be increased somewhat in the case of hard rubber. The point at which the rubber is bonded with the metal is not a weak point and is stronger than the actual rubber. If the surface under load is very large in relation to the surface not under load, this will produce a large modulus of elasticity and a very low level of deformation In this case an even higher level of stress is possible. The surface pressure can amount to up to 15-20 MPa.
If rubber is subject to excessive load, the deformation will be irreversible. This is called setting and is referred to as the permanent set or compression set. Good quality and correct vulcanisation of the rubber are the most important factors when it comes to limiting the setting process.
Further information
Rubber as a construction material
Rubber has special properties to offer in comparison with other construction materials. The elongation in some cases can be more than 1,000% and for the most part in the elastic range. Metals, by contrast, have very low strain values below the limit of elasticity.
Spring material
In the past, cork was usually used as a springy material, the springiness of which was due to compression and relaxation of the trapped air. The spring materials that are coming to the fore today are steel and rubber.
Principle Constellations
In principle, elastic intermediate layers, i.e. vibration dampers, are installed in practice for two different reasons: Practical considerations and protective considerations.

